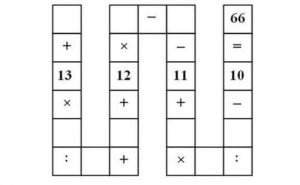
Les mathématiques ne passionnent en général pas grand monde, sauf qu’un problème de math donné à des enfants de CE2 agite internet depuis plusieurs jours, car très peu sont de gens sont capables de trouver la solution ! Pourquoi ne pas essayer ? On vous donne un petit coup de main, la réponse est 66 !
Un problème de math qui va vous occuper le weekend
Le Vietnam ne va pas faillir à sa réputation de l’un des pays avec le meilleur niveau en mathématique dans le monde, très loin devant la France où encore les Etats-Unis. La preuve qui stimule le web depuis quelques heures, est le problème de mathématique confié à des enfants de CE2 de l’école de Bao Loc, que peu d’adultes sont capables de réaliser.
Il s’agit d’un serpent Vietnamien dont quelques cases sont vides et qu’il faut remplir avec des chiffres allant de 1 à 9, pour obtenir un très long calcul dont le total est 66. Certaines personnes affirment, qu’il existe une centaine de solutions à ce problème et pourtant peu de gens parviennent à en trouver une seule ! Vous n’avez pas 8 ans, mais peut-être vous sentez-vous capable de relever le défi et de trouver la solution à ce problème de mathématique original ?

«il n’y a pas d’opération compliquée, c’est de l’arithmétique simple»
Malgré la simplicité, même des personnes ayant d’excellentes connaissances en math, n’arrivent pas à aller au bout de ce serpent Vietnamien. Il faut dire que pour remplir les 9 cases, avec un chiffre allant de 1 à 9, il y a 362880 possibilités… De quoi agiter les méninges de n’importe qui durant quelques heures…
Petit conseil d’arithmétique, que l’on oublie vite quand on arrête l’école. N’oubliez pas que les multiplications et les divisions sont prioritaires. 2+2×2=6 et non pas 8, comme beaucoup le pense. Tous à vos calculettes !
Dernière mise à jour le 20 août 2018